PointNet:The Pioneer of Point Cloud Deep Learning

Point Cloud Data

Point cloud data refers to a set of vectors in a 3D coordinate system. A normal point cloud object is usually with 2D shape (n, 3+X), where n is the number of points, 3 stands for 3D coordinates and X contains other features like color and orientation.

Fig.1 Point Cloud Data Visualization

Point cloud data has the following characteristics:

• Permutation Invariance: A point cloud object with $n$ points can be permuted in $n!$ different orders, but the point set always represents the same object no matter how they are permuted.
• Transformation Invariance: Classification and segmentation outputs should be unchanged if the object undergoes rigid transformations.
• Interaction among points: The points are from a space with a distance metric which means that points are not isolated.

To use point cloud data, Volumetric CNNs transform point data into volumes, but is constrained by its resolution due to data sparsity and computation cost of 3D convolution; Multiview CNNs try to render 3D point cloud or shapes into 2D images and apply 2D conv nets to
classify them, which is nontrivial to extend them to scene understanding or other 3D tasks such as point classification and shape completion.

PointNet

PointNet was first proposed in 2016 and is the first to directly use point cloud data for deep learning.It takes raw point cloud data as input for classification and segmentation.

PointNet Architecture

Fig.2 Overrall of PointNet

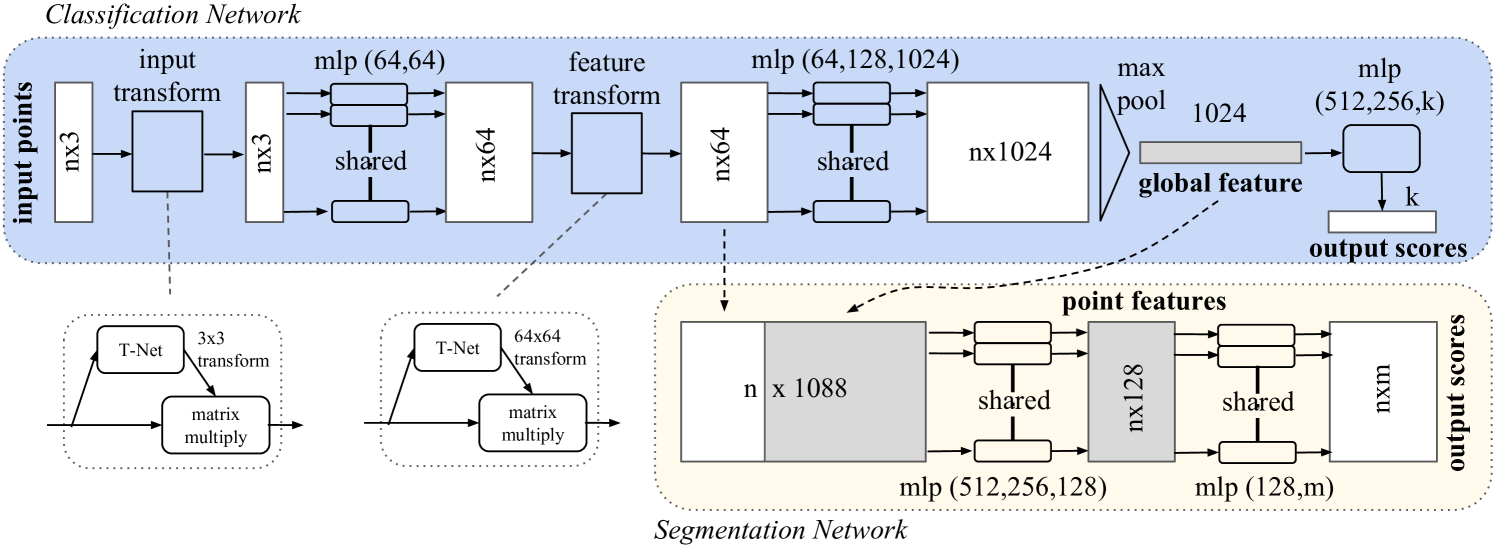
The classification network takes n points as input, applies input and feature transformations, and then aggregates point features by max pooling. The output is classification scores for k classes. The segmentation network is an extension to the classification net. It concatenates global and local features and outputs per point scores. “mlp” stands for multi-layer perceptron, numbers in bracket are layer sizes. Batchnorm is used for all layers with ReLU. Dropout layers are used for the last mlp in classification net.

By analyzing the architecture of PointNet above, we can divide PointNet into 2 stages: input & feature transform and certain task output. Noticeably, for each point cloud object, the number of points is usually different, so we need to sample a fixed number of points at first.Here we use a method called Farthest Point Sampling (FPS), which iteratively samples the farthest point and performs distance updating.

Given input points ${x_1, x_2, …, x_n}$, FPS choose a subset of points ${x_{i_1} , x_{i_2} , …, x_{i_m}}$, such that $x_{i_j}$ is the most distant point (in metric distance) from the set ${x_{i_1} , x_{i_2} , …, x_{i_{j-1}}}$ with regard to the rest points. Compared with random sampling, it has better coverage of the entire point set given the same number of centroids. FPS sampling strategy generates receptive fields in a data dependent manner.

Here’s the code of FPS:

def farthest_point_sample(point, npoint):
    """
    Input:
        xyz: pointcloud data, [N, D]
        npoint: number of samples
    Return:
        centroids: sampled pointcloud index, [npoint, D]
    """
    N, D = point.shape
    xyz = point[:,:3]
    centroids = np.zeros((npoint,))
    distance = np.ones((N,)) * 1e10
    farthest = np.random.randint(0, N)
    for i in range(npoint):
        centroids[i] = farthest
        centroid = xyz[farthest, :]
        dist = np.sum((xyz - centroid) ** 2, -1)
        mask = dist < distance
        distance[mask] = dist[mask]
        farthest = np.argmax(distance, -1)
    point = point[centroids.astype(np.int32)]
    return point

Task output

In order to analyze how to deal with permutation invariance more intuitively, we first discuss. As show in Fig.2, classfication head takes the output of feature transform with shape (n, 64) and the feature dimension is increased to 1024 by a mlp. After that, a max pool is excuted on dimension of number of points and we get global feature for each point with the length of 1024. Due to characteristics of max pool, the feature is permutation invariant. For segmantation, global feature is repeated by n times and concatenated with local feature (output of feature transform) to get point-wise feature.

Here’s the main code of this stage:

class PointNetEncoder(nn.Module):
    def __init__(self, global_feat=True, feature_transform=False, channel=3):
        super(PointNetEncoder, self).__init__()
        self.stn = STN3d(channel)
        self.conv1 = torch.nn.Conv1d(channel, 64, 1)
        self.conv2 = torch.nn.Conv1d(64, 128, 1)
        self.conv3 = torch.nn.Conv1d(128, 1024, 1)
        self.bn1 = nn.BatchNorm1d(64)
        self.bn2 = nn.BatchNorm1d(128)
        self.bn3 = nn.BatchNorm1d(1024)
        self.global_feat = global_feat
        self.feature_transform = feature_transform
        if self.feature_transform:
            self.fstn = STNkd(k=64)

    def forward(self, x):
        B, D, N = x.size()
        trans = self.stn(x)
        x = x.transpose(2, 1)
        if D > 3:
            feature = x[:, :, 3:]
            x = x[:, :, :3]
        x = torch.bmm(x, trans)
        if D > 3:
            x = torch.cat([x, feature], dim=2)
        x = x.transpose(2, 1)
        x = F.relu(self.bn1(self.conv1(x)))

        if self.feature_transform:
            trans_feat = self.fstn(x)
            x = x.transpose(2, 1)
            x = torch.bmm(x, trans_feat)
            x = x.transpose(2, 1)
        else:
            trans_feat = None

        pointfeat = x
        x = F.relu(self.bn2(self.conv2(x)))
        x = self.bn3(self.conv3(x))
        x = torch.max(x, 2, keepdim=True)[0]
        x = x.view(-1, 1024)
        if self.global_feat:
            return x, trans, trans_feat
        else:
            x = x.view(-1, 1024, 1).repeat(1, 1, N)
            return torch.cat([x, pointfeat], 1), trans, trans_feat

Where stn will be explained in next section.

Input & feature transform

For input transform, the PointNet model takes input with shape of (n, 3) and use a learnable T-Net to get an affine transformation matrix, then multiply the matrix and point cloud data. This stage is mainly to align the points to deal with the transformation invariance.

Here’s the code of T-Net (STN3d is similar):

class STNkd(nn.Module):
    def __init__(self, k=64):
        super(STNkd, self).__init__()
        self.conv1 = torch.nn.Conv1d(k, 64, 1)
        self.conv2 = torch.nn.Conv1d(64, 128, 1)
        self.conv3 = torch.nn.Conv1d(128, 1024, 1)
        self.fc1 = nn.Linear(1024, 512)
        self.fc2 = nn.Linear(512, 256)
        self.fc3 = nn.Linear(256, k * k)
        self.relu = nn.ReLU()

        self.bn1 = nn.BatchNorm1d(64)
        self.bn2 = nn.BatchNorm1d(128)
        self.bn3 = nn.BatchNorm1d(1024)
        self.bn4 = nn.BatchNorm1d(512)
        self.bn5 = nn.BatchNorm1d(256)

        self.k = k

    def forward(self, x):
        batchsize = x.size()[0]
        x = F.relu(self.bn1(self.conv1(x)))
        x = F.relu(self.bn2(self.conv2(x)))
        x = F.relu(self.bn3(self.conv3(x)))
        x = torch.max(x, 2, keepdim=True)[0]
        x = x.view(-1, 1024)

        x = F.relu(self.bn4(self.fc1(x)))
        x = F.relu(self.bn5(self.fc2(x)))
        x = self.fc3(x)

        iden = Variable(torch.from_numpy(np.eye(self.k).flatten().astype(np.float32))).view(1, self.k * self.k).repeat(
            batchsize, 1)
        if x.is_cuda:
            iden = iden.cuda()
        x = x + iden
        x = x.view(-1, self.k, self.k)
        return x

It is not difficult to find that T-Net also obtains permutation invariant affine transformation matrix through max pool. Transformation matrix in the feature space has much higher dimension than the input transform matrix, which greatly increases the difficulty of optimization, so the authors add a regularization term $L_{reg}=||I - AA^T||^2_F$ to make the transformation matrix A of the feature space as close to the orthogonal matrix as possible.

Reference

1. C. Qi et al, “PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation”, 2017 ↩
2. Pytorch_Pointnet_Pointnet2 ↩