Normalization——Batch Norm, Layer Norm, Instance Norm and Group Norm
Normalization——Batch Norm, Layer Norm, Instance Norm and Group Norm
Normalization
For a tensor with the shape of (N, C, D), where $N$ stands for batch-size, $C$ stands for features and D stands for feature map (for example, $D$ is H, W in computer vision), Z-Score Normalization of a certain dimension $l$ is
$$
\hat{z}^{l} = \frac{z^l - E(z^l)}{\sqrt{var(z^l)+\epsilon}}
$$
If some dimensions are ignored during normalization, the standardized data will retain the information between these dimensions; this may be a bit convoluted. Taking BN as an example, BN is standardized in each channel $C$, ignoring the pixel position, The sample number in the batch, so BN retains the association of data in these dimensions, but at the same time loses the data connection between channels.
Batch Normalization, Layer Normalization, Instance Normalization and Group Normalization are the most commonly used normalization methods based on Z-Score Normalization. They all consider and make a fuss about the input of the activation function, and normalize the input of the activation function in different ways.
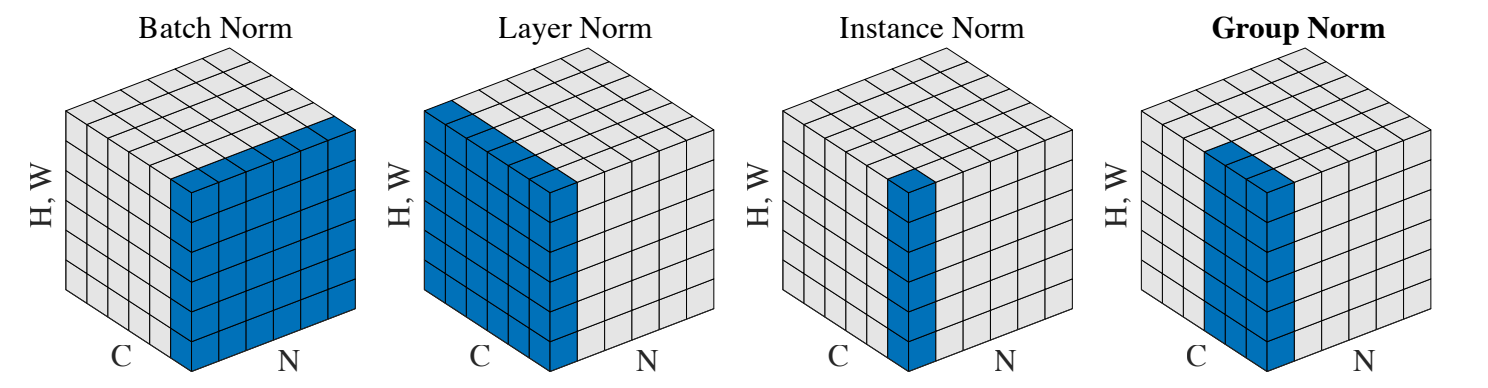
Normalization methods. Each subplot shows a feature map tensor, with N as the batch axis, C as the channel axis, and (H, W) as the spatial axes. The pixels in blue are normalized by the same mean and variance, computed by aggregating the values of these pixels
Batch Normalization
Motivation
In the process of deep neural network training, it is usually trained with each mini-batch input to the network, so that each batch has a different distribution, which makes the model training particularly difficult.
Internal Covariate Shift: In a deep neural network, the input of a middle layer is the output of the previous neural layer. Therefore, changes in the parameters of the neural layers before it lead to large differences in the distribution of its inputs. During the training process, the activation function will change the distribution of data in each layer. As the network deepens, this change (difference) will become larger and larger, making the model training particularly difficult, the convergence speed is very slow, and the gradient will disappear.
Method
BN takes channel $C$ as $l$. The standard normalization of the net input $z^l$will make its values concentrate around 0. If the sigmoid function is used, this value range is just close to the linear transformation range, which weakens the nonlinear nature of the neural network. Therefore, in order to normalize Without negatively affecting the representational power of the network, we can change the range of values through an additional scaling and translation transformation.
$$
\hat{z}^{l} = \frac{z^l - E(z^l)}{\sqrt{var(z^l)+\epsilon}} \odot \gamma + \beta \Leftarrow BN_{\gamma,\beta}(z^l)\quad where\quad l\quad is\quad C
$$
Where $\gamma$ and $\beta$ are learnable variables. BN is usually used after the fully connected layer or convolutional layer, before the activation function.
During training, the BN layer will use the mean and standard deviation of the data in each batch to standardize the samples in the batch each time; at the same time, the global mean and variance on the training set will be continuously updated and saved by means of sliding average.
While testing, normalize each data point on the test set with the mean and variance of the saved training set.
Discussion
Advantages
- Allows large learning rate
- Weaken the strong dependence on initialization and reduce the difficulty of weight initialization
- Avoid overfitting as each of mini-batch contain information from others and each mini-batch is sampled randomly
- Keep the mean and variance of the values in the hidden layer unchanged, control the distribution range of the data, and avoid gradient disappearance and gradient explosion
- Have the same regularization effect as dropout. In terms of regularization, dropout is generally used for fully connected layers, and BN is used for convolutional layers
- Alleviate internal covariate shift problem and increase training speed
Disadvantages
- The mean and variance are calculated on a batch each time. If the batch-size is too small, the calculated mean and variance are not enough to represent the entire data distribution.
- If the batch-size is too large, it will exceed the memory capacity; more epochs need to be run, resulting in a longer total training time; the direction of gradient descent will be fixed directly, making it difficult to update.
Layer Normalization
Motivation
For neural networks whose input distribution changes dynamically in the neural network, such as RNN, the BN operation cannot be applied, even if filled with specific characters, it will cause the problem of uneven distribution of some channels.
Method
Compared with BN, LN takes batch $N$ instead of channel $C$ as $l$.Other parts in LN are the same with BN
$$
\hat{z}^{l} = \frac{z^l - E(z^l)}{\sqrt{var(z^l)+\epsilon}} \odot \gamma + \beta \Leftarrow LN_{\gamma,\beta}(z^l)\quad where\quad l\quad is\quad N
$$
Discussion
LN does not require batch training, and can be normalized within a single piece of data. LN also does not depend on batch-size and the length of the input sequence, so it can be used in batch size 1 and RNN. The effect of LN on RNN is more obvious, but on CNN, the effect is not as good as BN.
Instance Normalization
Motivation
In image stylization, the generated result mainly depends on an image instance, and the mean and variance of each channel of the feature map will affect the style of the final generated image. Therefore, normalizing the entire batch is not suitable for image stylization, so normalizing H and W can speed up model convergence and maintain the independence between each image instance.
Method
Compared with BN, IN takes each channel $C$ of each batch $N$ instead of channel $C$ as $l$.Other parts in IN are the same with BN
$$
\hat{z}^{l} = \frac{z^l - E(z^l)}{\sqrt{var(z^l)+\epsilon}} \odot \gamma + \beta \Leftarrow LN_{\gamma,\beta}(z^l)\quad where\quad l\quad is\quad N * C
$$
Discussion
IN is a separate normalization operation for each channel in a sample, which is generally used for style migration, but if the feature map can use the correlation between channels, then IN is not suitable.
Group Normalization
Motivation
The proposed formula of GN is to solve the problem that BN has poor effect on small mini batch-size, and is suitable for tasks that occupy relatively large video memory, such as image segmentation. For this type of task, the batch size may only be a single digit, and no matter how large the video memory is, it will not be enough. When the batch size is a single digit, BN performs poorly, because there is no way to approximate the mean and standard deviation of the population through the amount of data of several samples. GN is also independent of batch, it is a compromise between LN and IN.
Method
GN divides channels of each sample into G groups. Compared with BN, GN takes each group $C / G$ of each batch $N$ instead of channel $C$ as $l$.Other parts in GN are the same with BN
$$
\hat{z}^{l} = \frac{z^l - E(z^l)}{\sqrt{var(z^l)+\epsilon}} \odot \gamma + \beta \Leftarrow LN_{\gamma,\beta}(z^l)\quad where\quad l\quad is\quad N * \frac{C}{G}
$$
Reference
- 深度学习基础 之 —- BN、LN、IN、GN、SN ↩
- Sergey Ioffe and Christian Szegedy. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In ICML, 2015. ↩
- Jimmy Lei Ba, Jamie Ryan Kiros, and Geoffrey E. Hinton. Layer normalization. arXiv:1607.06450, 2016. ↩
- Dmitry Ulyanov, Andrea Vedaldi, and Victor Lempitsky. Instance normalization: The missing ingredient for fast stylization. arXiv:1607.08022, 2016. ↩
- Yuxin Wu and Kaiming He. Group normalization. arXiv:1803.08494, 2018. ↩