Neural Radiance Fields

3D Shape Representations

Explicit Representation

The description of a scene is explicit, and the 3D representation of the scene can be seen directly, such as mesh, point cloud, voxel and volume which can directly visualize the corresponding scene.

Explicit representation will cause artifacts such as overlap because as it is usually discrete.

Implicit Representation

Usually a function is used to describe the scene geometry. Implicit means to use an MLP to simulate the function, such as inputting 3D space coordinates and outputting corresponding geometric information.

It is a continuous representation that is suitable for large resolution scenes and usually does not require 3D signals for supervision

Novel View Synthesis (NVS)

Novel View Synthesis (NVS) refers to the problem of capturing a scene from a novel angle Given a dense sampling of views.

NeRF

Fig.1 NeRF

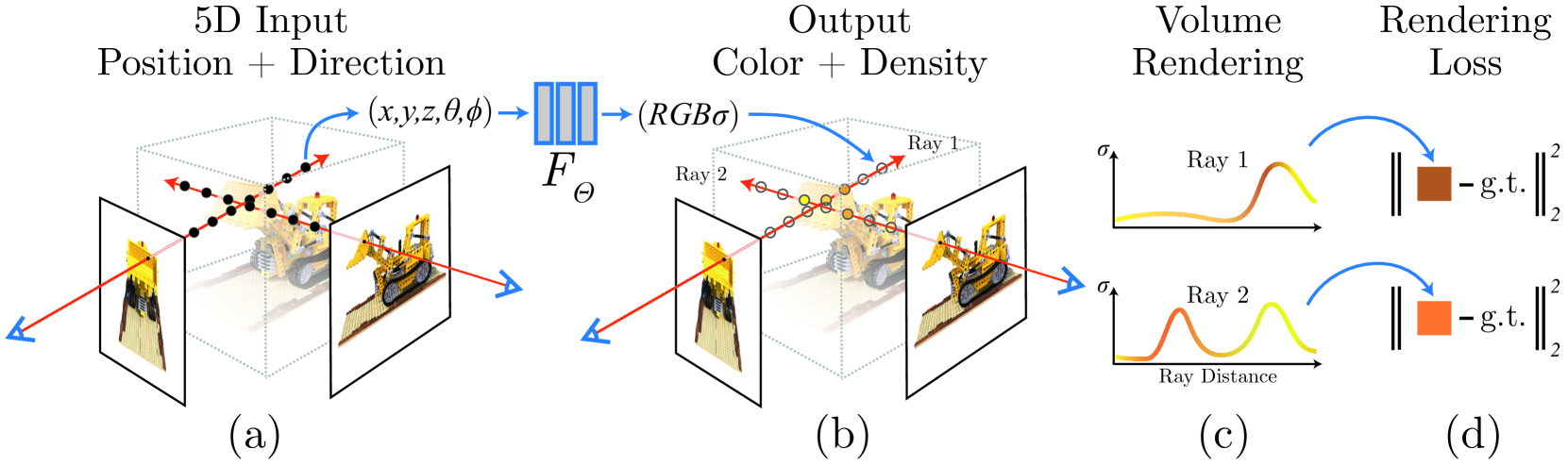
NeRF proposed a 5D neural radiance field (MLP) realize the implicit representation of complex scenes. The neural radiance field encodes the entire 3D scene into the parameters of the neural network.

To be able to render a scene from any new viewpoint, a neural network needs to learn at least the RGB color $(r, g, b)$ and volume density $\sigma$ of each point in space.

$$
(r, g, b, \sigma) = \text{MLP}(x, y, z, \theta, \phi)
$$

To optimize the MLP, based on the classic Volume rendering, a differentiable rendering process is proposed (using layered sampling to improve rendering efficiency). A positional encoding is proposed to map 5D coordinates to a high-dimensional space, which is convenient for MLP learning.

Volume Rendering

Suppose the camera is located at $\mathbf{O}$, and the light direction is $\mathbf{d}$, then the equation of the light is $\mathbf{r}(t)=\mathbf{O}+t\mathbf{d}$, where t represents the distance between $\mathbf{O}$ and a certain point on the ray, its predicted pixel color $C(\mathbf{r})$ is

\begin{equation} C(\mathbf{r}) = \int_{t_n}^{t_f}T(t)\sigma(\mathbf{r}(t))\mathbf{c}(\mathbf{r}(t),\mathbf{d})dt,\textrm{ where }T(t)=\exp{\left(-\int_{t_n}^{t}\sigma(\mathbf{r}(s))ds\right)} \end{equation}

$T(t)$ represents the proportion of light transmitted to the $t$ point, $\sigma(t)\mathrm{d}t$ Indicates the proportion of the light that will be blocked in a small neighborhood near the $t$ point. The multiplication of the two is the proportion of light that reaches $t$ and is blocked at point $t$, and then multiplied by the color $\textbf{c}(\textbf{r}(t), \textbf{d})$ is the contribution of this point to the final color of the light. The integration interval $[t_n, t_f]$ represents the closest intersection point $t_{near}$ and the farthest intersection point $t_{far}$ of the ray with the medium.

In actual calculation, we need to use discrete sums to approximate the integral value. That is, some discrete points are collected on the light, and their colors are weighted and summed.A stratified sampling approach is used where we partition $[t_n, t_f]$ into $N$ evenly-spaced bins and then draw one sample uniformly at random from within each bin:

$$
t_{i}\sim\mathcal{U}\left[ t_{n}+\frac{i-1}{N}(t_{f}-t_{n}), t_{n}+\frac{i}{N}(t_{f}-t_{n}) \right]
$$

Then we can use these samples to estimate $C(\mathbf{r})$ with the quadrature rule discussed in the volume rendering:

\begin{equation} \hat{C}(\mathbf{r}) = \sum _{i=1}^{N}T_{i}(1-\exp{(-\sigma _{i}\delta _{i}}))\mathbf{c}_{i}\, \textrm{ where }T_{i}=\exp{\left(-\sum _{j=1}^{i-1}\sigma _{j}\delta _{j}\right)} \end{equation}

where $\delta_i = t_{i+1} − t_i$ is the distance between adjacent samples. This function for calculating $\hat{C}(\mathbf{r})$ from the set of $(c_i , \sigma_i)$ values is trivially differentiable and reduces to traditional alpha compositing with alpha values $\alpha_i =(1-\exp{(-\sigma _{i}\delta _{i}}))$.

Optimizing a Neural Radiance Field

Positional Encoding

As deep networks are biased towards learning lower frequency functions and mapping the inputs to a higher dimensional space using high frequency functions before passing them to the network enables better fitting of data that contains high frequency variation, the network $F_{\Theta}$ is a composition of two functions ${F_{\mathrm{\Theta}}=F^{\prime}_{\mathrm{\Theta}}\circ\gamma}$, Here $\gamma$ is a mapping from $\mathbb{R}$ into a higher dimensional space $\mathbb{R}^{2L}$ the same as used in transformer, and $F^{\prime}_{\mathrm{\Theta}}$ is still simply a regular MLP.

This function is applied separately to each of the three coordinate values in $\mathbf{x}$ (which are normalized to lie in $[−1, 1]$) and to the three components of the Cartesian viewing direction unit vector $\mathbf{d}$ (which by construction lie in $[−1, 1]$). In NeRF, $L = 10$ for $\mathbf{x}$ and $L = 4$ for $\mathbf{d}$.

Hierarchical Volume Sampling

The rendering strategy of densely evaluating the neural radiance field network at $N$ query points along each camera ray is inefficient as free space and occluded regions that do not contribute to the rendered image are still sampled repeatedly. Thus, a hierarchical representation that increases rendering efficiency by allocating samples proportionally to their expected effect on the final rendering is used.

Instead of just using a single network to represent the scene, NeRF simultaneously optimize two networks: one “coarse” and one “fine”. First sample a set of $N_c$ locations using stratified sampling, and evaluate the “coarse” network at these locations as described before. Given the output of this “coarse” network, a more informed sampling of points are produced along each ray where samples are biased towards the relevant parts of the volume. To do this, the alpha composited color from the coarse network $\hat{C}(\mathbf{r})$ is rewrited as a weighted sum of all sampled colors $c_i$ along the ray:

$$
\hat{C}_{c}(\mathbf{r})=\sum_{i=1}^{N_{c}}w_{i}c_{i},\quad w_{i}=T_{i}(1-\exp{(-\sigma_{i}\delta_{i}))}
$$

Normalizing these weights as $\hat{w}_{i}=\frac{w_{i}}{\sum_{j=1}^{N_c}w_{j}}$ produces a piecewise-constant PDF along the ray and then sample a second set of $N_f$locations from this distribution using inverse transform sampling, evaluate the “fine” network using all $N_c+N_f$ samples. This procedure allocates more samples to regions expected to contain visible content, addressing a similar goal as importance sampling. In NeRF, $N_c = 64$ and $N_f = 128$.

Model Architecture

Fig.2 MLP in NeRF

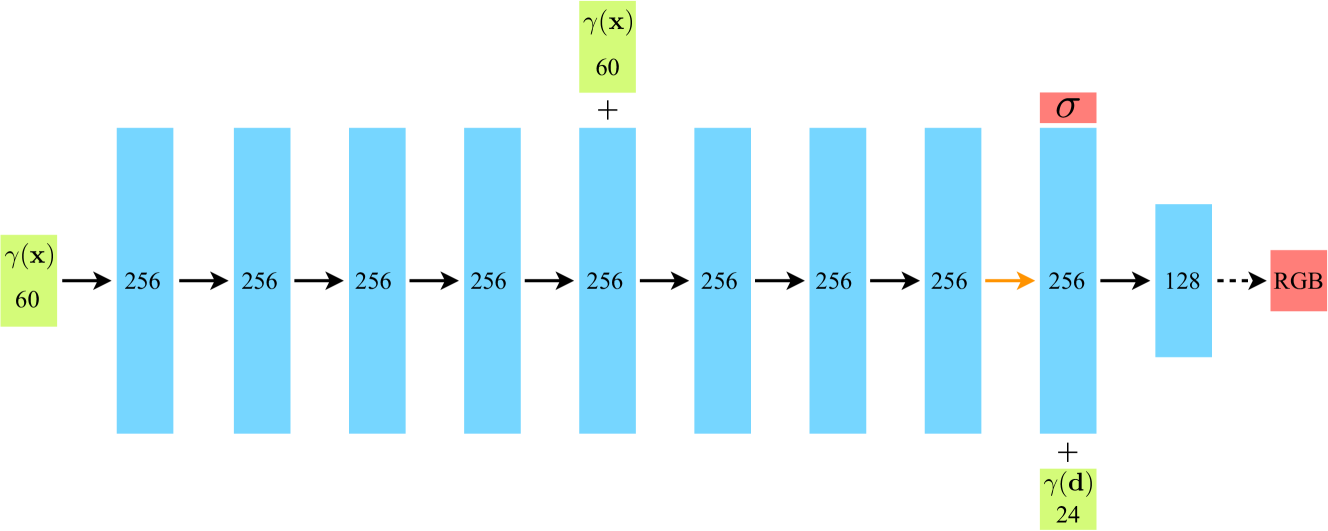
See Fig.2 . Input vectors are shown in green, intermediate hidden layers are shown in blue, output vectors are shown in red, and the number inside each block signifies the vector’s dimension. All layers are standard fully-connected layers, black arrows indicate layers with ReLU activations, orange arrows indicate layers with no activation, dashed black arrows indicate layers with sigmoid activation, and “+” denotes vector concatenation. The positional encoding of the input location $(\gamma(\mathbf{x}))$ is passed through 8 fully-connected ReLU layers, each with 256 channels. An additional layer outputs the volume density $\sigma$ (which is rectified using a ReLU to ensure that the output volume density is nonnegative) and a 256-dimensional feature vector. This feature vector is concatenated with the positional encoding of the input viewing direction $(\gamma(\mathbf{d}))$, and is processed by an additional fully-connected ReLU layer with 128 channels. A final layer (with a sigmoid activation) outputs the emitted RGB radiance at position $\mathbf{x}$, as viewed by a ray with direction $\mathbf{d}$.

The loss is simply the total squared error between the rendered and true pixel colors for both the coarse and fine renderings:

\begin{equation} \mathcal{L} = \sum_{\mathbf{r}\in \mathcal{R}}\left[ \left \lVert \hat{C}_{c}(\mathbf{r})-C(\mathbf{r})\right \rVert_{2}^{2}+\left \lVert \hat{C}_{f}(\mathbf{r})-C(\mathbf{r})\right \rVert_{2}^{2}\right] \end{equation}

Reference

1. Mildenhall, B., Srinivasan, P.P., Tancik, M., Barron, J.T., Ramamoorthi, R., & Ng, R. (2020). NeRF. Communications of the ACM, 65, 99 - 106. ↩
2. A Surge in NeRF ↩
3. 神经辐射场(NeRF)-代码无痛解读 ↩
4. NeRF（神经辐射场）有相关的物理（光学）原理支撑吗？ ↩