DreamFusion

Motivation

• Applying diffusion models to other modalities has been successful, but requires large amounts of modality-specific training data. 3D assets
  are currently designed by hand in modeling software like Blender and Maya3D, a process requiring a great deal of time and expertise. Text-to-3D generative models could lower the barrier to entry for novices and improve the workflow of experienced artists.

• GANs can learn controllable 3D generators from photographs of a single object category, by placing an adversarial loss on 2D image renderings of the output 3D object or scene . Though these approaches have yielded promising results on specific object categories such as faces, they have not yet been demonstrated to support arbitrary text.

• Dream Fields , which uses frozen image-text
  joint embedding models from CLIP and an optimization-based approach to train NeRFs, showed that pretrained 2D image-text models may be used for 3D synthesis, though 3D objects produced by this approach tend to lack realism and accuracy.

Differential Image Parameterization

Diffusion models trained on pixels have traditionally been used to sample only pixels. Dreamfusion wants to create 3D models that look like good images when rendered from random anglesare instead of being interested in sampling pixels.

Such models can be specified as a differentiable image parameterization (DIP), where a differentiable generator $g$ transforms parameters $\theta$ to create an image $\bf{x} = g(\theta)$. DIPs allow us to express constraints, optimize in more compact spaces (e.g. arbitrary resolution coordinate-based MLPs), or leverage more powerful optimization algorithms for traversing pixel space. For 3D, $\theta$ can be parameters of a 3D volume and $g$ can be a volumetric renderer.To learn these parameters, a loss function that can be applied to diffusion models is used.

Score Distillation Sampling

Fig.1 DDPM and Score Distillation Sampling

DreamFusion leverages the structure of diffusion models to enable tractable sampling via optimization —— a loss function that, when minimized, yields a sample. DreamFusion optimize over parameters $\theta$ such that $\bf{x} = g(\theta)$ looks like a sample from the frozen diffusion model. To perform this optimization, a differentiable loss function where plausible images have low loss, and implausible images have high loss is required.

While reusing the diffusion training loss to find modes of the learned conditional density $p(\bf{x}|y)$ in high dimensions are often far from typical samples, the multiscale nature of diffusion model training may help to avoid these pathologies.

Consider the training process of a ddpm which predicts the noise added at a certain timestep. For a pretrained ddpm with true noisy images as input, the predicted noise should be very close to real noise. Inversely, if those noisy images do not look like good images, there will be great difference between predicted noise and real noise.

Minimizing the diffusion training loss with respect to a generated datapoint $\bf{x} = g(\theta)$ gives $ \theta^{*} = \text{arg min} _{\theta}\mathcal{L}_{\text{Diff}}(\phi, \bf{x} = g(\theta))$ . In practice, this loss function did not produce realistic samples even when using an identity DIP where $\bf{x} = \theta$.

To understand the difficulties of this approach, consider the gradient of $\mathcal{L}_{\text{Diff}}$:

\begin{equation} \displaystyle\nabla_{\theta}\mathcal{L}_{\text{Diff}}(\phi,\mathbf{x}=g(\theta))=\mathbb{E}_{t,\epsilon}\Bigg{[}w(t)\underbrace{\left(\hat{\epsilon}_{\phi}({\mathbf{z}}_{t};y,t)-\epsilon\right)}_{\text{Noise Residual}}\underbrace{\frac{\partial\hat{\epsilon}_{\phi}({\mathbf{z}}_{t};y,t)}{\mathbf{z}_t}}_{\text{U-Net Jacobian}}\quad \underbrace{\frac{\partial\mathbf{x}}{\partial\theta}}_{\text{Generator Jacobian}}\Bigg{]} \end{equation}

Where the constant $\alpha _t\bf{I} = \partial \bf{z}_t/\partial \bf{x}$ is absorbed into $w(t)$. In practice, the U-Net Jacobian term is
expensive to compute (requires backpropagating through the diffusion model U-Net), and poorly conditioned for small noise levels as it is trained to approximate the scaled Hessian of the marginal density.Omitting the U-Net Jacobian term leads to an effective gradient for optimizing DIPs with diffusion models:

\begin{equation} \displaystyle\nabla_{\theta}\mathcal{L}_{\text{SDS}}(\phi,\mathbf{x}=g(\theta))\triangleq\mathbb{E}_{t,\epsilon}\left[w(t)\left(\hat{\epsilon}_{\phi}({\mathbf{z}}_{t};y,t)-\epsilon\right){\partial\mathbf{x}\over\partial\theta}\right] \end{equation}

Since the diffusion model directly predicts the update direction,there’s no need to backpropagate through the diffusion model; the model simply acts like an efficient, frozen critic that predicts image-space edits.

Empirically, the guidance weight $w$ is set to a large value for classifier-free guidance to improves quality.

The Dreamfusion Algorithm

Fig.2 The Dreamfusion Algorithm

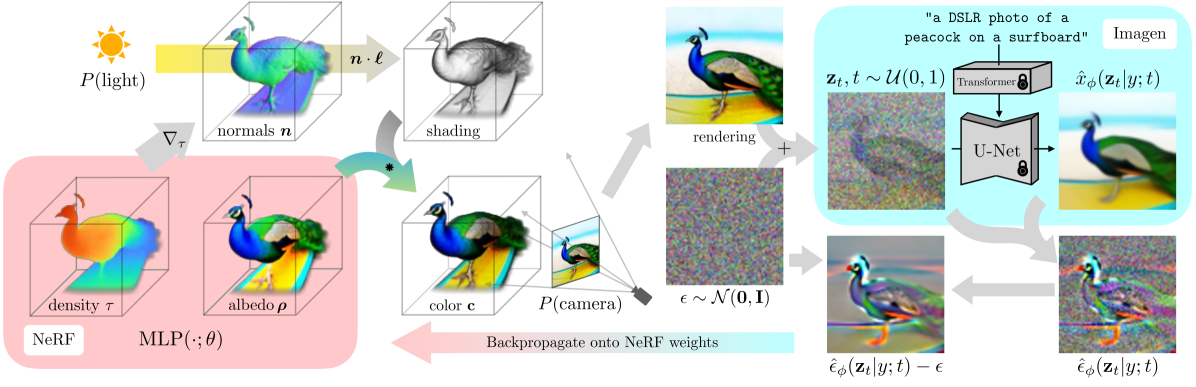
In DreamFusion, the Imagen model is chosen as the diffusion model.Only the pretrained $64\times 64$ base model (not the super-resolution cascade for generating higher-resolution images) is used with no modifications. To synthesize a scene from text, a model built on mip-NeRF 360 with random weights is initialized, then repeatedly render views of that NeRF from random camera positions and angles, using these renderings as the input to the score distillation loss function that wraps around Imagen.

Here is the pseudocode of the DreamFusion

params = generator.init()
opt_state = optimizer.init(params)
diffusion_model = diffusion.load_model()
for nstep in iterations:
    t = random.uniform(0., 1.)
    alpha_t, sigma_t = diffusion_model.get_coeffs(t)
    eps = random.normal(img_shape)
    x = generator(params, <other arguments>...) # Get an image observation.
    z_t = alpha_t * x + sigma_t * eps # Diffuse observation.
    epshat_t = diffusion_model.epshat(z_t, y, t) # Score function evaluation.
    g = grad(weight(t) * dot(stopgradient[epshat_t - eps], x), params)
    params, opt_state = optimizer.update(g, opt_state) # Update params with optimizer.
return params

Neural Rendering of a 3D Model

Shading. Traditional NeRF models emit radiance, which is RGB color conditioned on the ray direction from which the 3D point is being observed. In contrast, NeRF MLP in DreamFusion parameterizes the color of the surface itself, which is then lit by an illumination that can be controlled (a process commonly referred to as “shading”). An RGB albedo (the color of the material) is used for each point:

$$
(\tau, \mathbf{\rho}) = \text{MLP}(\mathbf{\mu};\theta)
$$

where $\tau$ is volumetric density. Calculating the final shaded output color for the 3D point requires a normal vector indicating the local orientation of the object’s geometry. This surface normal vector can be computed by normalizing the negative gradient of density $\tau$ with respect to the 3D coordinate :$ {n}=-\nabla_\tau / \left \lVert \nabla_\tau\right\rVert\ $. With each normal n and material albedo $\rho$ , assuming some point light source with 3D coordinate $l$ and color $\ell_{\rho}$ , and an ambient light color $\ell_a$, we can render each point along the ray using diffuse reflectance to produce a color $\bf{c}$ for each point:

$$
\mathbf{c}={\rho}\circ\left({\ell}_{\rho}\circ\operatorname{max}\left(0,{n}\cdot({\ell}-{\mu})/\left\lVert{\ell}-{\mu}\right\rVert\right)+{\ell}_{a}\right)
$$

With these colors and previously-generated densities, we approximate the volume rendering integral with the same rendering weights $w_i$ used in standard NeRF. It is beneficial to randomly replace the albedo color $\bf{c}$ with white $(1; 1; 1)$ to produce a “textureless” shaded output. This prevents the model from producing a degenerate solution in which scene content is drawn onto flat geometry to satisfy the text conditioning.

Scene Structure. Scene is represented within a fixed bounding sphere, and an environment map generated from a second MLP that takes positionally-encoded ray direction as input is used to compute a background color.

Geometry regularizers. A regularization penalty $\mathcal{L}_{orient} = \sum_{i}stop\_grad(w_i) \max(0;n_i\cdot v)^2$ on the opacity along each ray to prevent unneccesarily filling in of empty space .A modified version of the orientation loss $\mathcal{L}_{opacity} =\sqrt{\sum_i (w_i)^2 + 0.01}$ attempts to orient normals away from the camera so that the shading becomes darker

Reference

1. Poole, B., Jain, A., Barron, J.T., & Mildenhall, B. (2022). DreamFusion: Text-to-3D using 2D Diffusion. ArXiv, abs/2209.14988. ↩
2. DETAILS about DreamFusion: Text-to-3D using 2D Diffusion ↩