SDFusion

Abstract

In this work, we present a novel framework built to simplify 3D asset generation for amateur users. To enable interactive generation, our method supports a variety of input modalities that can be easily provided by a human, including images, text, partially observed shapes and combinations of these, further allowing to adjust the strength of each input. At the core of our approach is an encoderdecoder, compressing 3D shapes into a compact latent representation, upon which a diffusion model is learned. To enable a variety of multi-modal inputs, we employ taskspecific encoders with dropout followed by a cross-attention mechanism. Due to its flexibility, our model naturally supports a variety of tasks, outperforming prior works on shape completion, image-based 3D reconstruction, and text-to-3D. Most interestingly, our model can combine all these tasks into one swiss-army-knife tool, enabling the user to perform shape generation using incomplete shapes, images, and textual descriptions at the same time, providing the relative weights for each input and facilitating interactivity. Despite our approach being shape-only, we further show an efficient method to texture the generated shape using largescale text-to-image models.

Overview

Fig.1 SDFusion

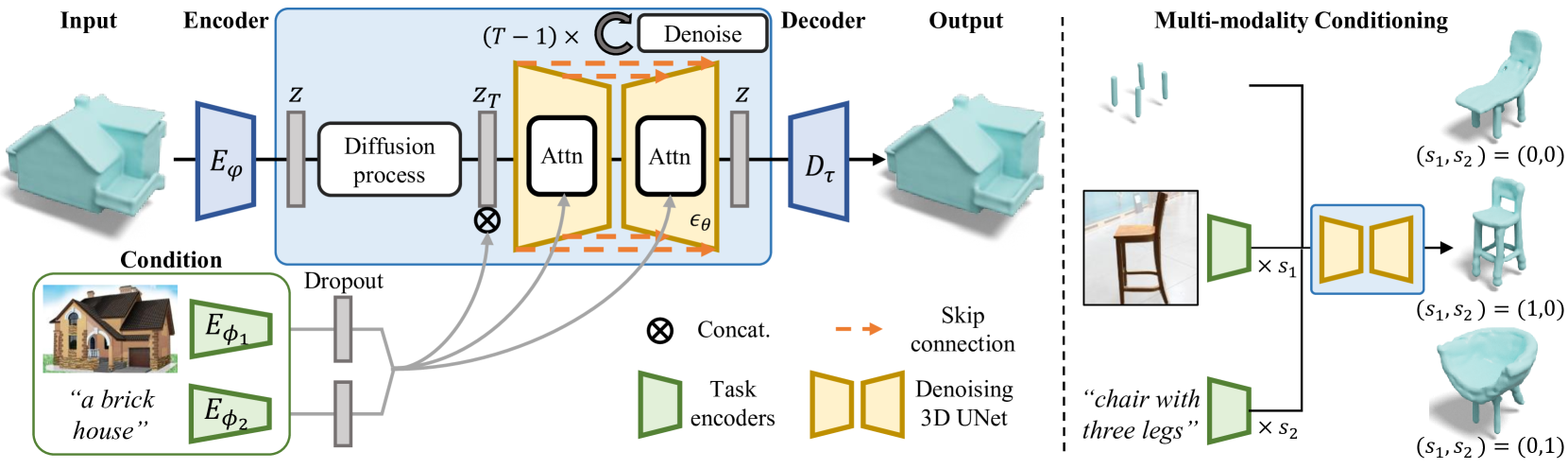
See Fig.1 . SDFusion takes signed distance function (SDFs) as input, which are known to represent well highresolution shapes with arbitrary topology. To side-step the issue that 3D representations are infamous for demanding high computational resources, an auto-encoder is utilized to compress 3D shapes into a more compact low-dimensional representation. Diffusion models are used to learn the probability distribution over the introduced latent space. Furthermore, SDFusion adopt taskspecific encoders and a cross-attention mechanism to support multiple conditioning inputs, and apply classifierfree guidance to enable flexible conditioning usage.

3D Shape Compression of SDF

To compress the 3D shape $\bf{X}$ into a lower-dimensional yet compact latent space, SDFusion leverages a 3D-variant of the VQ-VAE Specifically, the employed 3D VQ-VAE contains an encoder $E_{\varphi}$ to encode the 3D shape into the latent space, and a decoder $D_{\tau}$ to decode the latent vectors back to 3D space. Given an input shape represented via the T-SDF $\bf{X}\in \mathbb{R}^{D\times D\times D}$, then
$$
\displaystyle{\bf z}=E_{\varphi}({\bf X}),\quad\text{and}\quad{\bf X}^{\prime}=D_{\tau}(\text{VQ}({\bf z}))
$$

where $\bf{z} \in \mathbb{R}^{d\times d\times d}$ is the latent vector, latent dimension $d$ is smaller than 3D shape dimension $D$, and $\text{VQ}$ is the quantization step which maps the latent variable $\bf{z}$ to the nearest element in the codebook $\mathcal{Z}$. The encoder $E_{\varphi}$, decoder $D_{\tau}$ , and codebook $\mathcal{Z}$ are jointly optimized. The VQ-VAE is pre-trained with reconstruction loss, commitment loss, and VQ objective.

Latent Diffusion Model for SDF

Using the trained encoder Eφ, SDFs are encoded into a compact and low-dimensional latent variable ${\bf z}=E_{\varphi}({\bf X})$. Then a timeconditional 3D UNet $\epsilon_\theta$ is chosed as denoising model.

Learning the Conditional Distribution

SDFusion incorporats multiple conditional input modalities at once with task-specific encoders $E_{\varphi}$ and a cross-attention module. To further allow for more flexibility in controlling the distribution, classifier-free guidance is adopted to for conditional generation. The objective function reads as follows:

\begin{aligned} L(\theta , \{\phi_i\}) := \mathop {\mathbb{ E }} \limits_{\bf{z} , \bf{c} , \epsilon , t} \left [ ||{\epsilon - \epsilon _\theta ({\bf{z}}_t, t, F\{D\circ E{\phi_i}({\bf{c}}_i)\}) || }^2 \right ] \end{aligned}

where $E{\phi_i}(\bf{c}_i)$ is the task-specific encoder for the $i$th modality, $D$ is a dropout operation enabling classifier-free guidance, and $F$ is a feature aggregation function. In this work, $F$ refers to a simple concatenation.

At inference time, given conditions from multiple modalities, then

\begin{aligned} &\epsilon_\theta ({\bf{z}}_t, t, F\{E{\phi_i}~\forall i\}) = \epsilon_\theta ({\bf{z}}_t, t, \boldsymbol {\emptyset })+\\ & \sum_i s_i\left (\epsilon_\theta ({\bf{z}}_t, t, F\{E{\phi_i}({\bf{c}}_i), E{\phi _j}({\bf{c}}_j) : {\bf{c}}_j= \boldsymbol {\emptyset } ~\forall j\neq i\}) \right .\\ &\left .- \epsilon \theta ({\bf{z}}_t, t, \boldsymbol {\emptyset })\right ) \end{aligned}

where $s_i$ denotes the weight of conditions from the $i$th modality and $\phi$ denotes a condition filled with zeros. For shape completion, given a partial observation of a shape, SDFusion performs blended diffusion. For single-view 3D reconstruction, SDFusion adopts CLIP as the image encoder. For text-guided 3D generation, SDFusion adopts BERT as the text encoder.

3D Shape Texturing with a 2D Model

Fig.2 3D Shape Texturing

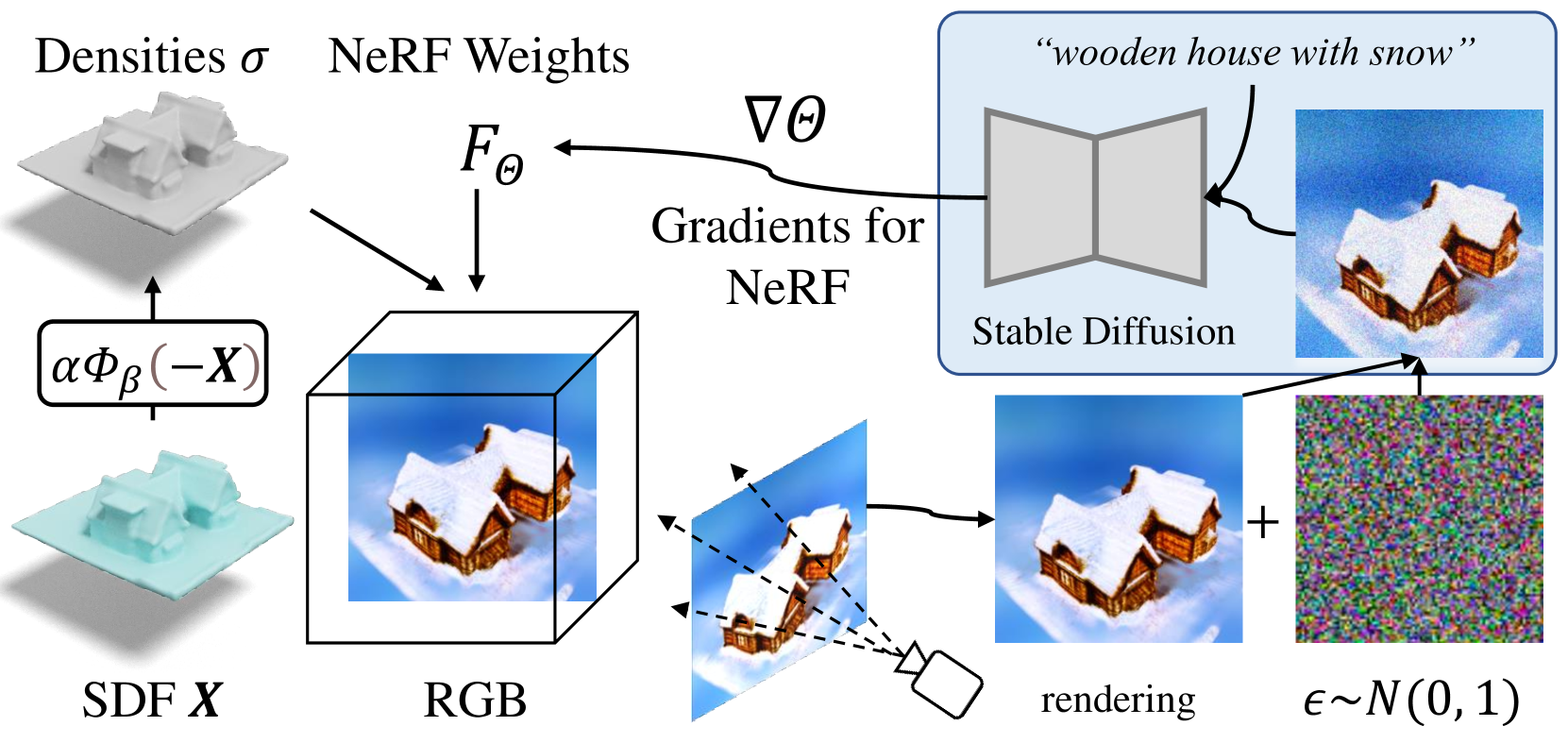
Starting from a generated T-SDF $\bf{X}$, then it is converted to a density tensor $\sigma$ by using VolSDF. After that, a 5D radiance field $F_\theta$ learns to obtain color $\bf{c}$ through scored distillation sampling (SDS) similar to DreamFusion.

Reference

1. Cheng, Y., Lee, H., Tulyakov, S., Schwing, A.G., & Gui, L. (2022). SDFusion: Multimodal 3D Shape Completion, Reconstruction, and Generation. ArXiv, abs/2212.04493. ↩