NeuralField-LDM
Abstract
Automatically generating high-quality real world 3D scenes is of enormous interest for applications such as virtual reality and robotics simulation. Towards this goal, we introduce NeuralField-LDM, a generative model capable of synthesizing complex 3D environments. We leverage Latent Diffusion Models that have been successfully utilized for efficient high-quality 2D content creation. We first train a scene auto-encoder to express a set of image and pose pairs as a neural field, represented as density and feature voxel grids that can be projected to produce novel views of the scene. To further compress this representation, we train a latent-autoencoder that maps the voxel grids to a set of latent representations. A hierarchical diffusion model is then fit to the latents to complete the scene generation pipeline. We achieve a substantial improvement over existing state-of-the-art scene generation models. Additionally, we show how NeuralField-LDM can be used for a variety of 3D content creation applications, including conditional scene generation, scene inpainting and scene style manipulation.
Overview
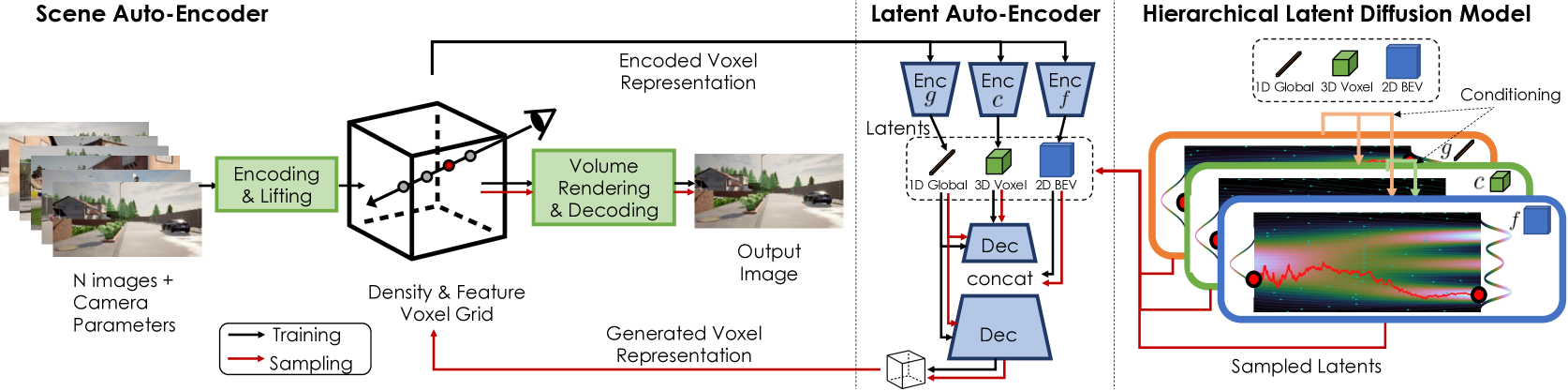
Overview of NeuralField-LDM. We first encode RGB images with camera poses into a neural field represented by density and feature voxel grids. We compress the neural field into smaller latent spaces and fit a hierarchical latent diffusion model on the latent space. Sampled latents can then be decoded into a neural field that can be rendered into a given viewpoint.
Scene Auto-Encoder
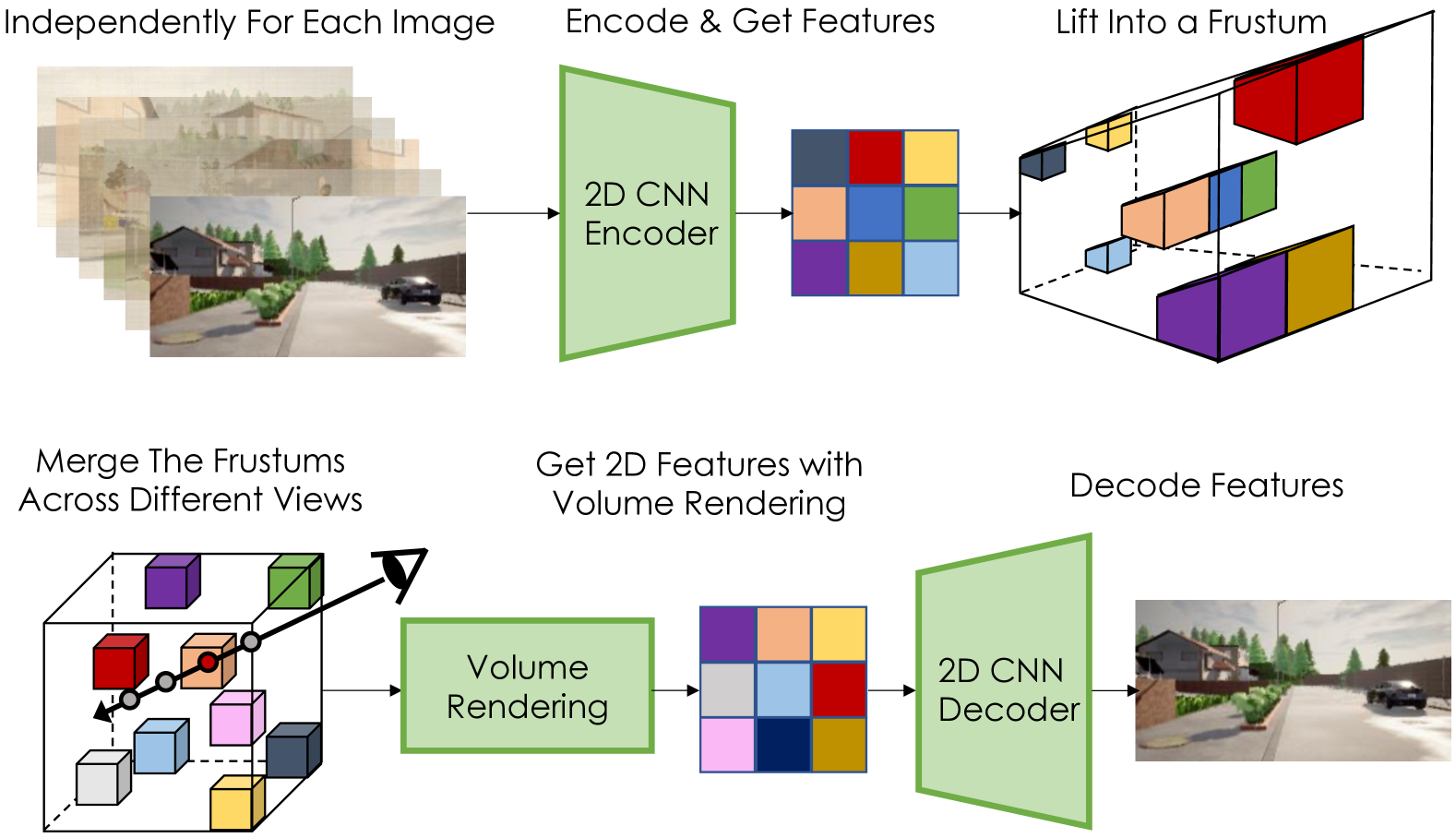
The goal of the scene auto-encoder is to obtain a 3D representation of the scene from input images by learning to reconstruct them. Each input image is processed with a 2D CNN then lifted up to 3D and merged into the shared voxel grids.
The scene encoder is a 2D CNN and processes each RGB image $i_{1..N}$ separately, producing a $R^{H\times W\times (D+C)}$ dimensional 2D tensor for each image, where $H$ and $W$ are smaller than $i$’s size. Then a discrete frustum of size $H \times W \times D$ with the camera poses $\mathcal{k}$ for each image is defined. Take the $d’$th channel of the CNN’s output at pixel $(h, w)$ as the density value of the frustum entry at $(h, w, d)$. The occupancy weight $O$ of each element $(h, w, d)$ in the frustum using the density values $\sigma \geq 0$ is :
$$
O(h, w, d) = \exp (-\sum_{j=0}^{d-1}\sigma_{(h, w, j)}\delta_{j})(1-\exp (-\sigma_{d}\delta_{d}))
$$
where $\delta_j$ is the distance between each depth in the frustum. Using the occupancy weights, put the last $C$ channels of the CNN’s output into the frustum $F$ to get:
$$
F(h, w, d) = [ O(h, w, d)\phi(h, w), \sigma(h, w, d) ]
$$
where $\phi(h, w)$ denotes the $C$-channeled feature vector at pixel $(h, w)$ which is scaled by $O(h, w, d)$ for $F$ at depth $d$. After the frustum of each view being constructed, they are transformed into world coordinates and fused into a shared 3D neural field $V$ which contains both $V_{\text{feat}}$ and $V_{\text{density}}$. For each voxel indexed by $(x, y, z)$, the density and feature are defined as mean of the corresponding frustum entries. 2D features are extracted by using the camera poses $\mathcal{k}$ to project on $V$ and then fed into a CNN decoder that produces the output image.
The scane auto-encoding pipeline is trained with an image reconstruction loss and a depth supervision loss.
Latent Voxel Auto-Encoder
$V_{\text{feat}}$ and $V_{\text{density}}$ are concatenated along the channel dimension and thein encoded into a hierarchy of three latents: 1D global latent $g$, 3D coarse latent $c$, and 2D fine latent $f$. The intuition for this design is that $g$ is responsible for representing the global properties of the scene, such as the time of the day, $c$ represents coarse 3D scene structure, and $f$ is a 2D tensor with the same horizontal size $X × Y$ as $V$ , which gives further details for each location $(x, y)$ in BEV perspective. The camera trajectory information are concatenated to $g$ and also being learned to sample.
The encoder is a 2D CNN taking $V$ as input, the vertical axis of which is concatenated along the channel dimension. The decoder uses conditional group normalization layers with $g$ as the conditioning variable. LAE is trained with the voxel reconstruction loss along with the image reconstruction loss with a fixed scene auto-encoder.
Hierarchical Latent Diffusion Models
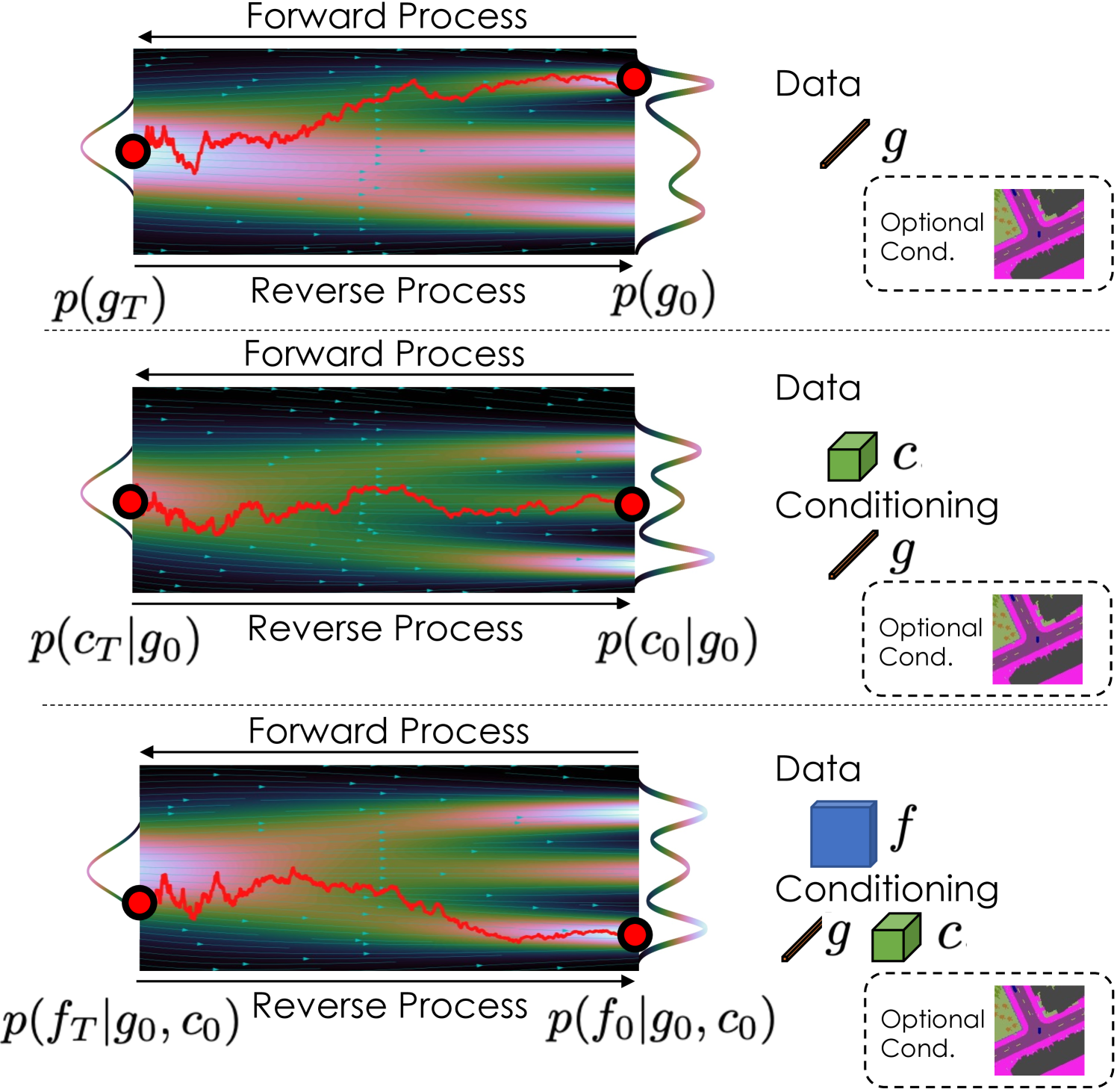
Given the latent variables $g$, $c$, $f$ that represent a voxel-based scene representation $V$ ,the generative model based on DDPM is defined as $p(V, g, c, f)=p(V|g, c, f)p(f|g, c)p(c|g)p(g)$. $g$ is conditioned by conditional group normalization layers and $c$ is conditioned by being interpolated and concatenated to the input of $p(f|g, c)$.
Post-Optimizing Generated Neural Fields
The initially generated voxels, $V$, canbe further optimized by rendering viewpoints from the scene and applying SDS loss on each image independently.