Zero-1-to-3:Zero-shot One Image to 3D Object
Abstract
We introduce Zero-1-to-3, a framework for changing the camera viewpoint of an object given just a single RGB image. To perform novel view synthesis in this under-constrained setting, we capitalize on the geometric priors that large-scale diffusion models learn about natural images. Our conditional diffusion model uses a synthetic dataset to learn controls of the relative camera viewpoint, which allow new images to be generated of the same object under a specified camera transformation. Even though it is trained on a synthetic dataset, our model retains a strong zero-shot generalization ability to out-of-distribution datasets as well as in-the-wild images, including impressionist paintings. Our viewpoint-conditioned diffusion approach can further be used for the task of 3D reconstruction from a single image. Qualitative and quantitative experiments show that our method significantly outperforms state-of-the-art single-view 3D reconstruction and novel view synthesis models by leveraging Internet-scale pre-training.
Overview
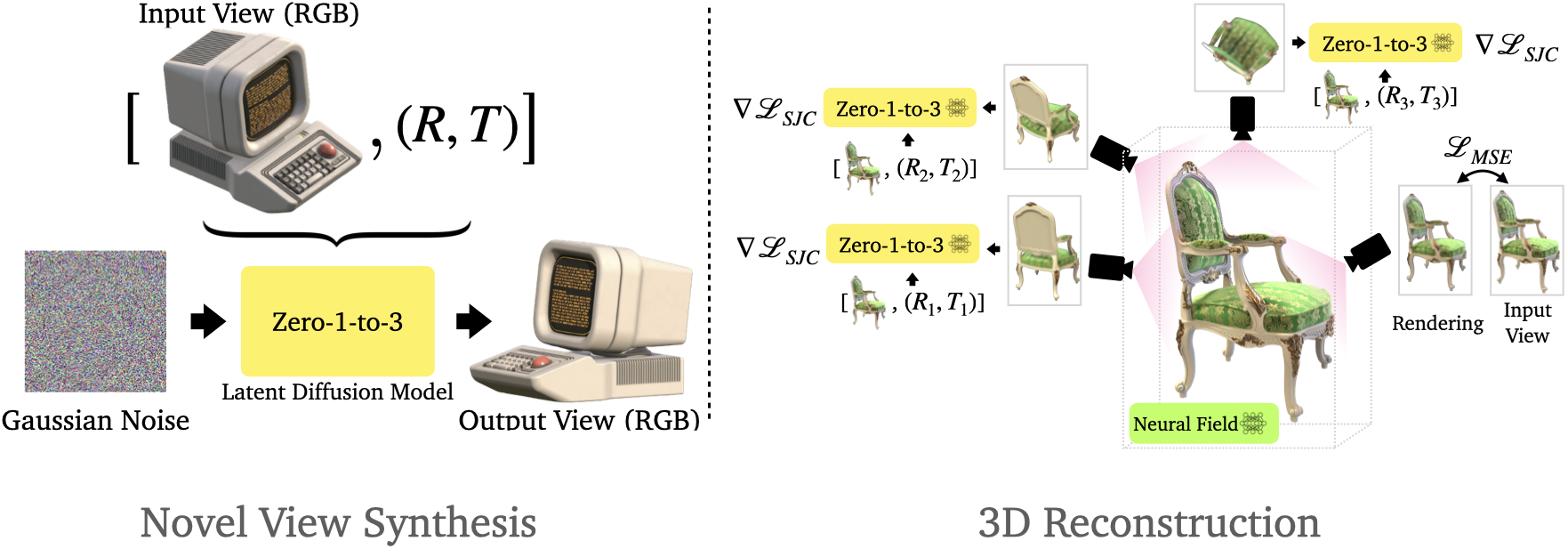
Given a single RGB image $x \in \mathbb{R}^{H\times W\times 3}$ of an object, the model synthesizes an image of the object from a different camera viewpoint:
$$
\hat{x}_{R, T} = f(x, R, T)
$$
where $\hat{x}_{R,T}$ is the synthesized image and ${R} \in \mathbb{R}^{3\times3}$ and ${T} \in \mathbb{R}^{3}$ are the relative camera rotation and translation of the desired viewpoint, respectively.
Learning to Control Camera Viewpoint
Since diffusion models have been trained on internetscale data, their support of the natural image distribution likely covers most viewpoints for most objects, but these viewpoints cannot be controlled in the pre-trained models. Zero123 aims to o teach the model a mechanism to control the camera extrinsics with which a photo is captured so that unlock the ability to perform novel view synthesis. To this end, given a dataset of paired images and their relative camera extrinsics $\{x, x_{(R, T)}, R, T\}$, Zero123 is fine-tuned from a pre-trained diffusion model Stable Diffusion. This fine-tuning allows controls to be “bolted on” and the diffusion model can retain the ability to generate photorealistic images, except now with control of viewpoints. This compositionality establishes zero-shot capabilities in the model, where the final model can synthesize new views for object classes that lack 3D assets and never appear in the fine-tuning set.
View-Conditioned Diffusion
3D reconstruction from a single image requires both lowlevel perception (depth, shading, texture, etc.) and highlevel understanding (type, function, structure, etc.). Therefore, On one hand, a CLIP embedding of the input image is concatenated with $(R, T)$ to form a “posed CLIP” embedding $c(x, R, T)$ as the condition of diffusion U-Net, which provides high-level semantic information of the input image. On the other hand, the input image is channel-concatenated with the image being denoised, assisting the model in keeping the identity and
details of the object being synthesized. To be able to apply classifier-free guidance the input image and the posed CLIP embedding are setting a null vector randomly, and the conditional information is scaled during inference.
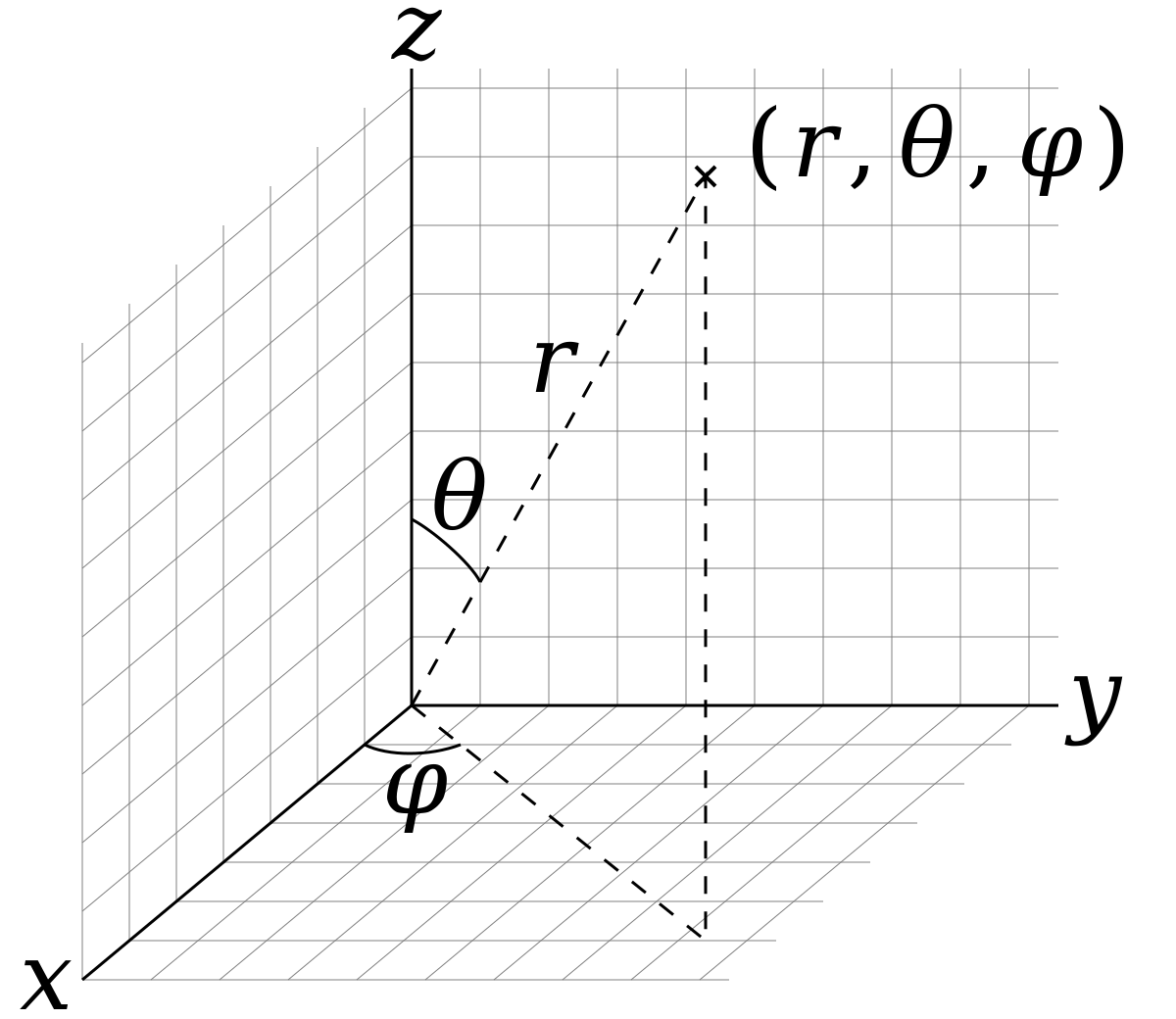
In fact, a spherical coordinate system is used to represent camera locations and their relative transformations. Thus, During training, when two images from different viewpoints are sampled, let their camera locations be $(\theta_1, \phi_1, r_21)$ and $(\theta_2, \phi_2, r_2)$. Their relative camera transformation is $(\theta_1-\theta_2, \phi_1-\phi_2, r_1-r_2)$. What’s more, the azimuth angle is encoded with $\phi \rightarrow [\sin (\phi), \cos (\phi)]$ due its incontinuity. So actually, the image CLIP embedding (dimension 768) and the pose vector $[\Delta \theta, \sin (\Delta \phi), \cos (\Delta \phi), \Delta r]$ are concatenated and and fed into another fully-connected layer $(772 \rightarrow 768)$ to ensure compatibility with the diffusion model architecture. The learning rate of this layer is scaled up to be $10\times$ larger than the other layers.