LoRA:Low-Rank Adaptation of LLMs
Abstract
An important paradigm of natural language processing consists of large-scale pre-training on general domain data and adaptation to particular tasks or domains. As we pre-train larger models, full fine-tuning, which retrains all model parameters, becomes less feasible Using GPT-3 175B as an example – deploying independent instances of fine-tuned models, each with 175B parameters, is prohibitively expensive. We propose Low-Rank Adaptation, or LoRA, which freezes the pre-trained model weights and injects trainable rank decomposition matrices into each layer of the Transformer architecture, greatly reducing the number of trainable parameters for downstream tasks. Compared to GPT-3 175B fine-tuned with Adam, LoRA can reduce the number of trainable parameters by a factor of 10,000 and the GPU memory requirement by a factor of 3. LoRA performs on-par or better than fine-tuning in model quality on RoBERTa, DeBERTa, GPT-2, and GPT-3, despite having fewer trainable parameters, a higher training throughput, and, unlike adapters, no additional inference latency. We also provide an empirical investigation into rank-deficiency in language model adaptation, which sheds light on the efficacy of LoRA. We release a package that facilitates the integration of LoRA with PyTorch models and provide our implementations and model checkpoints for RoBERTa, DeBERTa, and GPT-2 at https://github.com/microsoft/LoRA.
Low-Rank-Parametrize Update Matrices
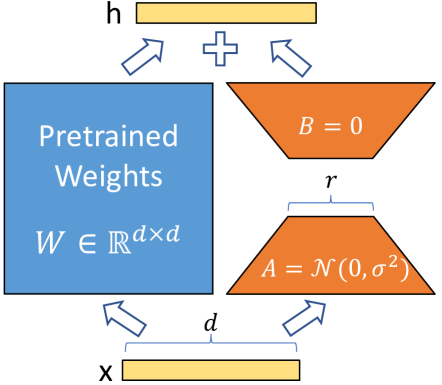
The weight matrices of dense layers in a neural network typically have full-rank. According to previous research, when adapting to a specific task, the pre-trained language models have a low “instrisic dimension” and can still learn efficiently despite a random projection to a smaller subspace. Inspired by this, LoRA comes from the hypothesis that the updates to the weights also have a low “intrinsic rank” during adaptation. For a pre-trained weight matrix $W_0 \in \mathbb{R}^{d\times k}$, LoRA constrains its update by representing the latter with a low-rank decomposition $W_0 + \Delta W = W_0 + BA$, where $B \in \mathbb{R}^{d\times r},A \in \mathbb{R}^{r\times k}$, and the rank $r \ll \min(d,k)$. During training, $W_0$ is frozen and does not receive gradient updates, while $A$ and $B$ contain trainable parameters. Note both $W_0$ and $\Delta W = BA$ are multiplied with the same input, and their respective output vectors are summed coordinate-wise. For $h = W_0x$, then :
$$
h=W_0x+\Delta Wx=W_0x+BAx
$$
See Fig.1, A is initialized by random Gaussian initialization and B is zero initialized, so $\Delta W = BA$ is zero at the beginning of training. $\Delta Wx$ can be scaled by $\frac{\alpha}{r}$ , where $\alpha$ is a constant in $r$. This scaling helps to reduce the need to retune hyperparameters when $r$ varies.