SparseNeuS
Abstract
We introduce SparseNeuS, a novel neural rendering based method for the task of surface reconstruction from multi-view images. This task becomes more difficult when only sparse images are provided as input, a scenario where existing neural reconstruction approaches usually produce incomplete or distorted results. Moreover, their inability of generalizing to unseen new scenes impedes their application in practice. Contrarily, SparseNeuS can generalize to new scenes and work well with sparse images (as few as 2 or 3). SparseNeuS adopts signed distance function (SDF) as the surface representation, and learns generalizable priors from image features by introducing geometry encoding volumes for generic surface prediction. Moreover, several strategies are introduced to effectively leverage sparse views for high-quality reconstruction, including 1) a multi-level geometry reasoning framework to recover the surfaces in a coarse-to-fine manner; 2) a multi-scale color blending scheme for more reliable color prediction; 3) a consistency-aware fine-tuning scheme to control the inconsistent regions caused by occlusion and noise. Extensive experiments demonstrate that our approach not only outperforms the state-of-the-art methods, but also exhibits good efficiency, generalizability, and flexibility.
Overview
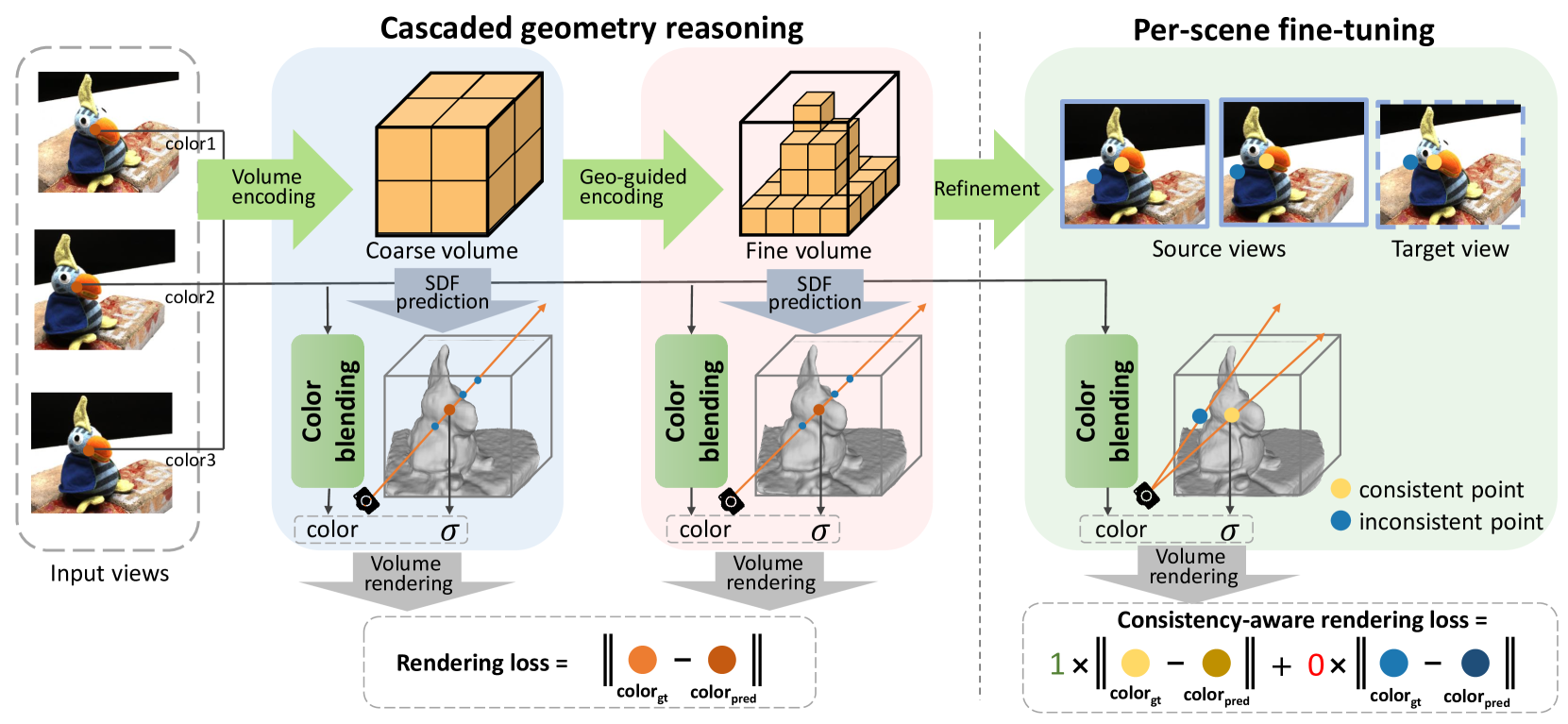
Given a few views with known camera parameters, SparseNeuS first constructs cascaded geometry encoding volumes that encode local geometry surface information, and recover surfaces from the volumes in a coarse-to-fine manner. SparseNeuS secondly leverages a multi-scale color blending module to predict colors by aggregating information from input images, and then combines the estimated geometry with predicted colors to render synthesized views using volume rendering. Finally, a consistencyaware fine-tuning scheme is proposed to further improve the obtained geometry with fine-grained details.
Geometry Reasoning
SparseNeuS constructs cascaded geometry encoding volumes of two different resolutions for geometry reasoning, which aggregates image features to encode the information of local geometry. Specially, the coarse geometry is first extracted from a geometry encoding volume of low resolution, and then it is used to guide the geometry reasoning of the fine level.
Geometry Encoding Volume
For the scene captured by $N$ input images $\{ I_{i} \}_{i=0}^{N-1}$, a bounding box which can cover the region of interests is first estimated. The bounding box is defined in the camera coordinate system of the centered input image, and then grided into regular voxels. To construct a geometry encoding volume $M$, 2D feature maps $\{F_{i}\}_{i=0}^{N-1}$ are extracted from the input images $\{I_{i}\}_{i=0}^{N-1}$ by a 2D feature extraction network. Next, with the camera parameters of one image $I$, each vertex $v$ of the bounding box is projected to each feature map $F_{i}$ and gots its features $F_{i}(\pi _{i}(v))$ by interpolation, where $\pi_{i}(v)$ denotes the projected pixel location of $F_{i}$ For simplicity, $F_{i}(\pi_{i}(v))$ is abbreviated as $F_{i}(v)$. Initialized by a cost volume $B$ and aggregated by a sparse 3D CNN $\psi$, the geometry encoding volume $M$ is constructed using all the projected features $\{F_{i}\}_{i=0}^{N-1}$ of each vertex:
$$
M = \psi(B), \quad B=\text{Var}(\{F_{i}\}_{i=0}^{N-1})
$$
Surface Extraction
Given an arbitrary 3D location $q$, an MLP network $f_{\theta}$ takes the combination of the 3D coordinate and its corresponding interpolated features of geometry encoding volume $M(q)$ as input, to predict the Signed Distance Function (SDF) $s(q)$ for surface representation. Specially, positional encoding PE is applied on its 3D coordinates, and the surface extraction operation is expressed as: $s(q) = f_{\theta}(\text{PE}(q), M(q))$.
Cascaded Volumes Scheme
For balancing the computational efficiency and reconstruction accuracy, SparseNeuS constructs cascaded geometry encoding volumes of two resolutions to perform geometry reasoning in a coarse-to-fine manner. A coarse geometry encoding volume is first constructed to infer the fundamental geometry, which presents the global structure of the scene but is relatively less accurate due to limited volume resolution. Guided by the obtained coarse geometry, a fine level geometry encoding volume is constructed to further refine the surface details. Numerous vertices far from the coarse surfaces can be discarded in the fine-level volume, which significantly reduces the computational memory burden and improves efficiency.
Appearance Prediction
Given an arbitrary 3D location $q$ on a ray with direction $d$, it is difficult for a network to directly regress color values for rendering novel views with those limited information. Thus, SparseNeuS predicts blending weights of the input images to generate new colors. A location $q$ is first projected to the input images to obtain the corresponding colors $\{I_i(q)\}^{N−1}_{i=0}$. Then the colors from different views are blended together as the predicted color of $q$ using the estimated blending weights.
Blending Weights
SparseNeuS first projects $q$ onto the feature maps $\{F_{i}\}_{i=0}^{N-1}$ to extract the corresponding features $\{F_{i}(q)\}_{i=0}^{N-1}$ using bilinear interpolation. Then the mean and variance of the features $\{F_{i}(q)\}_{i=0}^{N-1}$ from different views to capture the global photographic consistency information. Each feature $F_i(q)$ is concatenated with the mean and variance together, and then fed into a tiny MLP network to generate a new feature $F’(q)$. Next, the new feature $F’(q)$, the viewing direction of the query ray relative to the viewing direction of the $i$-th input image $\Delta d_i=d−d_i$ , and the trilinearly interpolated volume encoding feature $M(q)$ into an MLP network $f_c$ to generate blending weight: $w^q_i = f_c(F’_i(q), M(q), \Delta d_i)$. Finally, blending weights $\{w^q_i\}^{N−1}_{i=0}$ are normalized using a Softmax operator.
Color Blending
Pixel-based. With the obtained blending weights, the color $c_q$ of a 3D location $q$ is predicted as the weighted sum of its projected colors $\{I_i(q)\}^{N−1}_{i=0}$ on the input images. The color and SDF values of 3D points sampled on the ray are predicted to render the color of the query ray. The color and SDF values of the sampled points are aggregated to obtain the final colors of the ray using SDF based volume rendering. Although supervision on the colors rendered by pixel-based blending already induces effective geometry reasoning, the information of a pixel is local and lacks contextual information, thus usually leading to inconsistent surface patches when input is sparse.
Patch-based. To enforce the synthesized colors and ground truth colors to be contextually consistent not only in pixel level but also in patch level and reduce the amount of computation, SparseNeuS leverages local surface plane assumption and homography transformation to achieve a more efficient implementation.
The key idea is to estimate a local plane of a sampled point to efficiently derive the local patch. Given a sampled point $q$, the normal direction $n_q$ can be estimated by compute the spatial gradient, i.e., $n_q = \Delta s(q)$. Then, SparseNeuS samples a set of points on the local plane $(q, n_q)$, projects the sampled points to each view, and obtains the colors by interpolation on each input image. All the points on the local plane share the same blending weights with $q$, and thus only one query of the blending weights is needed. The local plane assumption,which considers the neighboring geometric information of a query 3D position, encodes contextual information of local patches and enforces better geometric consistency. By adopting patch-based volume rendering, synthesized regions contain more global information than single pixels, thus producing more informative and consistent shape context, especially in the regions with weak texture and changing intensity.
Volume Rendering
Volume rendering is operated similarly to NeRF:
$$
U(r) = \sum_{i=1}^{M}T_{i}(1-\exp(\sigma_{i}))u_i, \quad \text{where}\quad T_i=\exp(-\sum_{j=1}^{i-1}\sigma_i)
$$
Where $r$ represents a certain ray, $U(r)$ denotes Pixel-based color $C(r)$ or Patch-based color $P(r)$, $u_i$ is similar to $U(r)$ except $i$ representing a certain point sampled on the ray and densities $\sigma_i$ is converted from sdf values $s_i$ by Neus.
Per-scene Fine-tuning
To avoid inaccurate outliers and lack of subtle details caused by the limited information in the sparse input views and the high diversity and complexity of different scenes, a novel fine-tuning scheme, which is conditioned on the inferred geometry, is used to reconstruct subtle details and generate finer-grained surfaces.
Fine-tuning Networks
In the fine-tuning, SparseNeuS directly optimizes the obtained fine-level geometry encoding volume and the signed distance function (SDF) network $f_{\theta}$, while the 2D feature extraction network and 3D sparse CNN networks are discarded. Moreover, the CNN based blending network used in the generic setting is replaced by a tiny MLP network. Although the CNN based network can be also used in per-scene fine-tuning, a new tiny MLP can speed up the fine-tuning without loss of performance since the MLP is much smaller than the CNN based network. The MLP network still outputs blending weights $\{w^q_i\}^{N−1}_{i=0}$ of a query 3D position $q$, but it takes the input as the combination of 3D coordinate $q$, the surface normal $n_q$, the ray direction $d$, the predicted SDF $s(q)$, and the interpolated feature of the geometry encoding volume $M(q)$. Specially, positional encoding PE is applied on the 3D position $q$ and the ray direction $d$. The MLP network $f’_c$ is defined as $\{w^q_i\}^{N−1}_{i=0}= f’_c(\text{PE}(q),\text{PE}(d), nq, s(q), M(q))$, where $\{w^q_i\}^{N−1}_{i=0}$ are the predicted blending weights, and $N$ is the number of input images.
Consistency-aware Color Loss
in multi-view stereo, 3D surface points often do not have consistent projections across different views, since the projections may be occluded or contaminated by image noises. As a result, the errors of these regions suffer from sub-optima, and the predicted surfaces of the regions are always inaccurate and distorted. To tackle this problem, a consistency-aware color loss is used to automatically detect the regions lacking consistent projections and exclude these regions in the optimization:
Where $\mathbb{R}$ is the set of all query rays, $O (r)$ is the sum of accumulated weights along the ray $r$ obtained by volume rendering, $C (r)$ and $\hat{C} (r)$ are the rendered and ground truth pixel-based colors of the query ray respectively, $P (r)$ and $\hat{P} (r)$ are the rendered and ground truth patch-based colors of the query ray respectively, and $D_{\text{pix}}(L1 Loss)$ and $D_{\text{pat}}$(NCC Loss) are the loss metrics of the rendered pixel color and rendered patch colors respectively.
The rationale behind this formulation is, the points with inconsistent projections always have relatively large color errors that cannot be minimized in the optimization. Therefore, if the color errors are difficult to be minimized in optimization, the loss forces the sum of the accumulated weights $O (r)$ to be zero, such that the inconsistent regions will be excluded in the optimization. To control the level of consistency, SparseNeuS uses two logistic regularization terms: decreasing the ratio $\frac{\lambda_1}{\lambda_0}$ will lead to more regions being kept; otherwise, more regions are excluded and the surfaces are cleaner.
Training Loss
By enforcing the consistency of the synthesized colors and ground truth colors, the training of SparseNeuS does not rely on 3D ground-truth shapes. The overall loss function is defined as a weighted sum of the three loss terms:
$$
\mathcal{L}=\mathcal{L}_{\text{color }}+\alpha\mathcal{L}_{\text{eik}}+\beta\mathcal{L}_{\text{sparse}}
$$
Actually, in the early stage of generic training, the estimated geometry is relatively inaccurate, and 3D surface points may have large errors, where the errors do not provide clear clues on whether the regions are radiance consistent or not. Thus, only duiring the stage of generic training, an Eikonal term is applied on the sampled points to regularize the SDF values derived from the surface prediction network $f_{\theta}$ :
$$
\mathcal{L}_{eik}=\frac{1}{\left|\mathbb{Q}\right|}\sum_{q\in\mathbb{Q}}\left({\left|\nabla f_{\theta}\left(q\right)\right|}_{2}-1\right)^{2}
$$
and a sparseness regularization term to penalize the uncontrollable free surfaces caused by lack of supervising the invisible query samples behind the visible surfaces to enable compact geometry surfaces:
$$
\mathcal{L}_{sparse}=\frac{1}{\left|\mathbb{Q}\right|}\sum_{q\in\mathbb{Q}}\exp\left(-\tau\cdot\left|s(q)\right|\right)
$$
Where $\tau$ is a hyperparamter to rescale the SDF value.